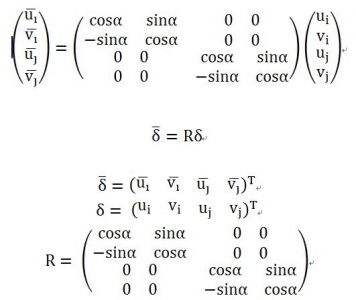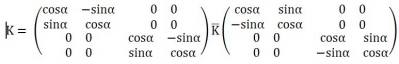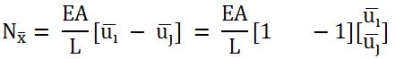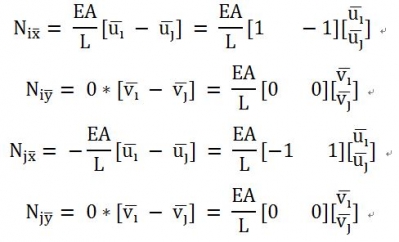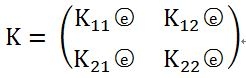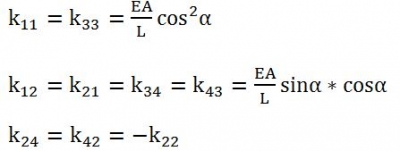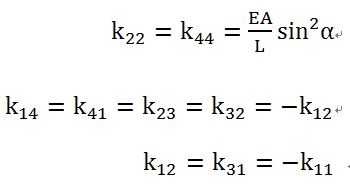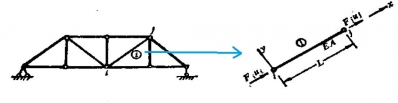
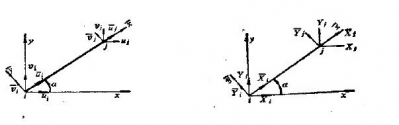
考慮位于總體坐標(biāo)系xiy平面內(nèi)的任意桿,左端為i,右端為j,桿軸與x軸夾角為α,桿的局部坐標(biāo)系xiy , 設(shè)結(jié)點(diǎn)i處的位移在局部坐標(biāo)系中表示為ui , vi  ,在總體坐標(biāo)系中表示為ui  vi , 結(jié)點(diǎn)j處同樣表示為uj , vj,uj  vj  如下圖

由幾何關(guān)系，可得

設(shè)定局部坐標(biāo)系與總體坐標(biāo)系間的夾角αα ,以逆時(shí)針為正,順時(shí)針為負(fù),。

將上式寫成矩陣形式有

2）結(jié)點(diǎn)力的坐標(biāo)變換（單元坐標(biāo)系、總體坐標(biāo)系）

3）剛度矩陣的坐標(biāo)變換

此時(shí)，局部剛度與整體剛度就有了轉(zhuǎn)換關(guān)系式

4）求解單元在整體坐標(biāo)系下剛度矩陣

目前我們的研究對象的特點(diǎn)是：只有沿著軸向的位移才產(chǎn)生應(yīng)力，即只存在軸向剛度。

假設(shè)軸向變形為△，單元內(nèi)力為N，由胡克定律可知：△=NL/EA，變形幾何關(guān)系可知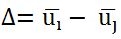

在局部坐標(biāo)系下，變形與單元內(nèi)力關(guān)系可表示為 

又由于桿單元內(nèi)部受力處處相等。那么節(jié)點(diǎn)受到的內(nèi)力可表示為

寫成矩陣形式

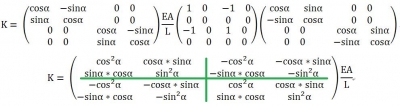
我們回過頭來看整體剛度K

   分塊表示 

5）求解單元在整體坐標(biāo)系下剛度矩陣方程

F=Kδ

6）形成結(jié)構(gòu)整體剛度矩陣方程

待續(xù)